Crittografia e numeri primi. Certo, dobbiamo riconoscerlo; tra chi si occupa di marketing il tema della privacy viene visto come un problema in più da risolvere. Un limite imposto che ci limita nell’utilizzo di targetizzazioni sempre più sofisticate per le nostre campagne.
In realtà, la privacy intesa come libertà di parlare privatamente ad un interlocutore, è tutto il contrario; potrebbe essere perfino un atto di libertà, un modo di utilizzare uno strumento potentissimo per dire quello che vogliamo veramente dire senza timore di incappare in qualsiasi censura.
Art is the earliest form of encryption.
Monaristw
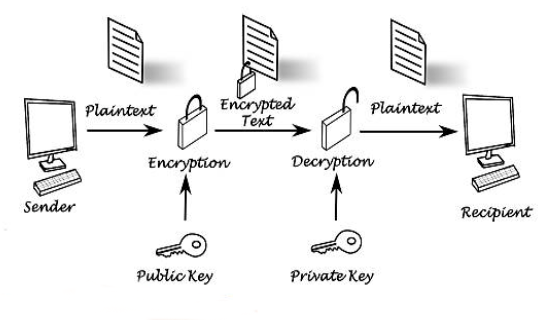
La crittografia ovvero la tecnica di poter cifrare i messaggi senza che altri (oltre mittente e destinatario) li possano interpretare, si sviluppa in diversi modi. Quella più diffusa è l’utilizzo di una chiave per ciascun partecipante alla comunicazione e utilizzarle per crittazione (al momento dell’invio) e relativa decrittazione (al momento della ricezione).
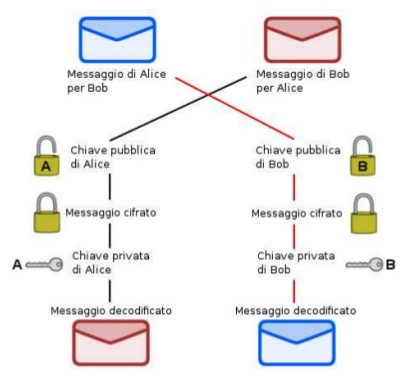
Il sistema di crittografia più utilizzato è il PGP Pretty Good Privacy, diventato un vero e proprio standard con il suo sistema di crittografia asimmetrica. In pratica ogni utente di PGP crea una chiave pubblica ed una privata. Se qualcuno vuole inviare un messaggio, utilizzerà la chiave pubblica del destinatario. A questo punto si potrà decriptarlo solo usando la corrispondente chiave privata.
È evidente che ora la criticità del processo sta proprio nelle chiavi; quanto sono sicure? Siamo sicuri che adottando tecniche come il metodo di forza bruta non si riesce a scoprire le chiavi? Questi non sono dei veri rischi, se si considera che per rivelare una chiave PGP, un calcolatore di grandi dimensioni potrebbe impiegare un tempo pari a diverse migliaia d’anni.
Per creare le chiavi spesso si utilizza il prodotto tra due numeri primi di grandi dimensioni. Dal risultato finale è quindi praticamente impossibile (in tempi umani) risalire ai due prodotti.
Ma come possiamo velocizzare le procedure in modo da essere certi che i numeri utilizzati siano dei “primi”? Per questo ci viene in soccorso un teorema sviluppato nel 1641 dal magistrato francese Pierre de Fermat. Questo singolare personaggio venne chiamato come “il principe dei dilettanti”, in quanto esercitava la professione di magistrato e studiava matematica per diletto nel tempo libero.
Per l’identificazione dei numeri primi, si utilizza il “piccolo teorema di Format”: se p è un numero primo, allora per ogni numero intero a, ap=a(mod p). Se si calcola ap per qualsiasi numero a e non si ottiene il valore a (mod p), allora si può affermare che p non è primo. Senza questo Teorema per capire se 18.313 è effettivamente un numero primo si doveva procedere a diverse prove sulle divisioni. Su questo numero si può ancora fare, ma ve la immaginate una serie di diverse centinaia di numeri da verificare con una decina di cifre ciascuno…
The government doesn’t want any system of transmitting information to remain unbroken, unless it’s under its own control.
Isaac Asimov, “Tales of the Black Widowers”
Crittografia e numeri primi
Per approfondimenti sulla crittografia, si può partire dal sito OpenPGP, perché come al solito la pratica aiuta la comprensione.
Poi abbiamo trovato degli stimoli su “La privacy digitale e i Teoremi di Format”, prima uscita della collana “La matematica che trasforma il mondo”.
Per una vista sui vari tipi di crittografia, può essere utile l’articolo “Come funziona la crittografia e quali sono i nuovi modelli permessi dall’ai”.